소수 판별 알고리즘
알고리즘을 공부하면서 어떤수에 대해 소수를 판별할때 1은 소수가 아니므로 2부터 해당수까지 약수 여부를 모두 검토하는 알고리즘을 사용해보았습니다. 문제를 풀면서 시간 초과가 발생하여 확인해본결과 모든 수를 돌면서 약수 여부를 판단하는 알고리즘은 시간복잡도상 O(N)이여서 비효율적이라고 합니다. 이런경우에는 해당 수의 제곱근까지만 검증을 하면 시간복잡도상 O(N^(1/2))로 더욱 효율적이게 됩니다.
아래는 소수 판별시 제곱근까지 검증한 알고리즘 코드(JAVA)입니다.
import java.util.*;
public class PrimeNumber {
public static boolean isPrimeNumber(int num) {
for(int i = 2; i<=(int)Math.sqrt(num); i++){
if(num % i == 0){
return false;
}
}
return true;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
if(isPrimeNumber(num)){
System.out.println(num + " is PrimeNumber");
}
else{
System.out.println(num + " isn't PrimeNumber");
}
}
}
2부터 소수를 판별하고자 하는 수의 제곱근까지 반복문을 돌리면서 확인하였습니다.
하지만 소수를 판별하고자 하는 숫자가 많다면 에라토스테네스의 체를 사용하는것이 좋습니다.
에라토스테네스의 체는 많은 숫자중에 소수를 빠르게 구할수 있게 해주는 유용한 알고리즘입니다.
에라토스테네스의체
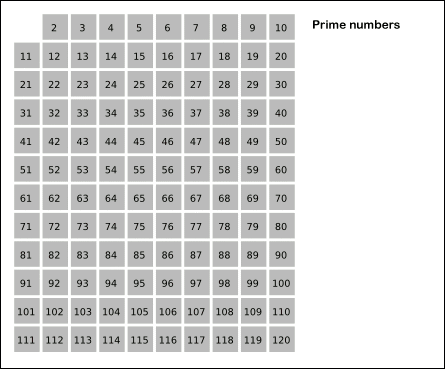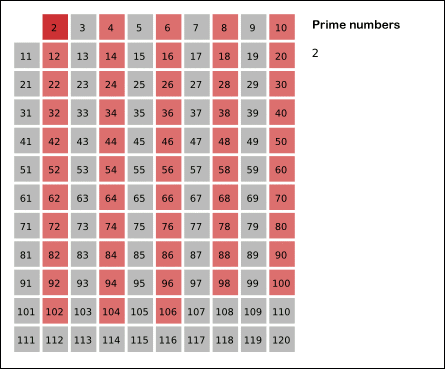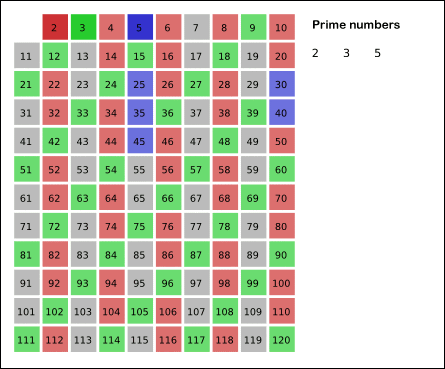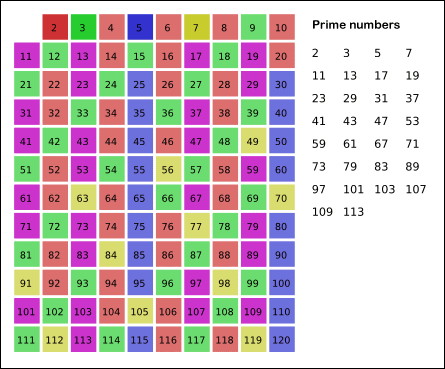
에라토스테네스의 체는 수학자 에라토스테네스가 만들어낸 소수를 찾는 방법으로써 체로 걸러 소수를 찾아낸다하여 에라토스테네스의 체라고 부릅니다.
소수(Prime Number)는 1과 자기 자신이외의 자연수로는 나눌수 없는 1보다 큰 자연수입니다.
에라토스테네스의 체는 범위가 주어지고 그 범위내에 있는 모든 소수를 찾아내는 경우에 많이 쓰입니다.
 Reference By Wikipedia
Reference By Wikipedia
1은 소수가 아니므로 제외하고 2부터 순차적으로 배수를 걸러가면서 소수를 찾는 알고리즘입니다.
소스코드는 아래와 같습니다.
import java.util.Scanner;
public class eratosthenes {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int range = sc.nextInt();
int result = 0;
int [] arr = new int[range+1];
for(int i = 2; i<=range; i++){
if(arr[i] == 0){
result++;
}
for(int j = 2 * i; j <= range; j += i){
arr[j] = 1;
}
}
System.out.println("소수의 개수는 " + result);
}
}
0을 기본으로 2부터 시작하여 배수에 1을 입력하여 배수를 걸러내어 기본값인 0의 개수로 소수의 개수를 판별하는 알고리즘입니다.